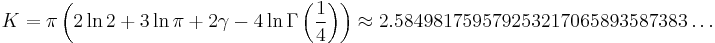Sierpiński's constant
Sierpiński's constant is a mathematical constant usually denoted as K. One way of defining it is by limiting the expression:
where r2(k) is a number of representations of k as a sum of the form a2 + b2 for natural a and b.
Its value is:
See also
External links
- http://www.scenta.co.uk/tcaep/science/constant/details/sierpinskisconstant.xml
- http://pi.lacim.uqam.ca/piDATA/sierpinski.txt - Sierpiński's constant up to 2000th decimal digit.
- Weisstein, Eric W., "Sierpinski Constant" from MathWorld.
- Sloane's A062089 . The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
![K=\lim_{n \to \infty}\left[\sum_{k=1}^{n}{r_2(k)\over k} - \pi\ln n\right]](/2012-wikipedia_en_all_nopic_01_2012/I/05c1914b8986cf6395c3fb4a5d713c89.png)